 GEMS:
GEMS:  GEMS:
GEMS: This test aims at demonstrating how GEM-Selektor calculates molal
activities (including pH and pe) and activity coefficients of charged
and neutral aqueous species and of water-solvent. Details on used
equations are provided in GEMS documentation (Activity-Coeffs.pdf file).
The test Process simulators also show how the values of equilibrium
constants of any reactions between dependent components included in the
system can be retrieved from activities, molalities and external
activity coefficients using the respective mass action expressions of
those reactions e.g. as function of ionic strength. One particular
conclusion that can be drawn from the test is that ignoring water
(activity) in solubility products of solids may lead to a significant
bias at high aqueous electrolyte concentrations.
The project system is constructed from independent components Ca,
Cl, H, Na, Nit, O, S and Zz (Nit is atmospheric nitrogen and Zz is
electrical charge). Phases and dependent components with their
thermodynamic data were extracted from GEMS default thermodynamic data
base (some irrelevant phases and components were removed from the
project to keep it smaller and simpler). Results provided in the
project were computed at 1 bar pressure and 25 C temperature (of
course, the users are encouraged to run examples at other
temperatures).
The recipe of the start system with SysEq record key "NaCl-dep:G:nacl:0:0:1:25:0:" is
set up from 1000 g of H2O, 10 g of CaO, 0.1 moles of gypsum (on System
DComp page); 0.1 mol NaCl; 0.01 mol of O2 and 2 mol of Nit (on System
IComp page). Calculation of this system using the built-in extended
Debye Hueckel (Helgeson) equation with calculation of activity
coefficient of H2O (as set in the project) results in the presence of
stable Portlandite and Gypsum phases with ca. 1 mol of gas mixture
(mainly N2) and 55.622485 mol of aqueous solution with pH = 12.454, pe
= 7.818 and IS = 0.207 m. Aqueous speciation is given on the screenshot
below.
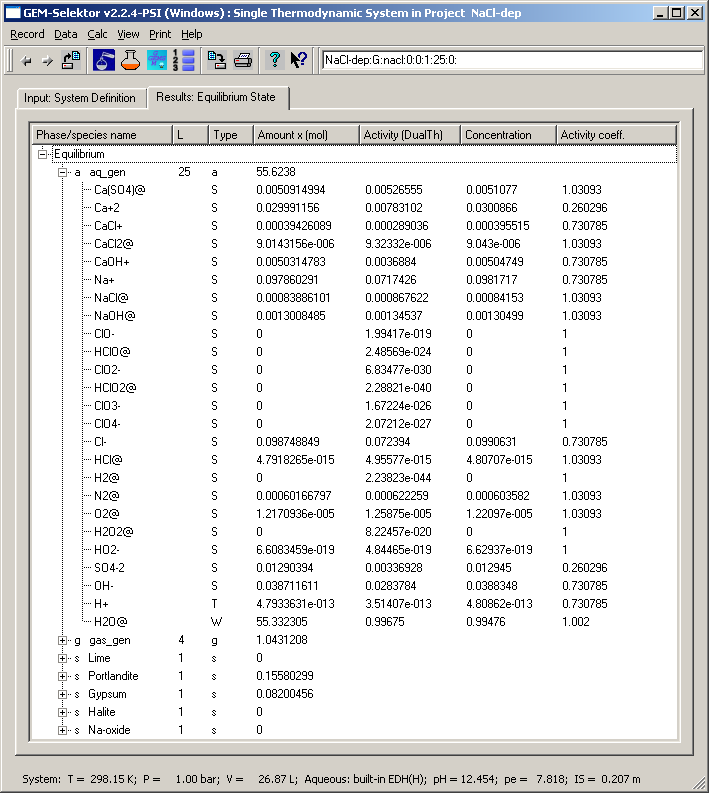
Numbers in the "Concentration" column are molalities and in the
"Activity coeff." column - molal external activity coefficients of
aqueous species. Their product must be (almost) equal to the respective
number in the "Activity (DualTh)" column. Let us check this for e.g.
Na+ ion:
0.0981717 * 0.730785 = 0.0717424. This compares well with a(Na+) =
0.0717426, the difference is in 6th digit, which corresponds to
numerical precision of GEM IPM convergence.
Let us calculate the solubility product Ks of portlandite according
to the reaction: Ca(OH)2(s) = Ca+2 + 2(OH-). The respective LMA
expression is Ks = a(Ca+2) * a(OH-)^2 (activity of stable portlandite
equals to 1.0). Substituting respective numbers from the "Activity
(DualTh)" column, we obtain: Ks = 0.00783102 * (0.0283784)^2 =
6.306583 or log10Ks = -5.200206. To compare, let us
calculate the standard Gibbs energy difference for this reaction (the
Go values are accessible through "Data" "Thermodynamic data ..." menu
command in the "MTparm" window: DrG = -552790 + 2* -157270
- -897013 = +29683 J/mol. Keeping in mind that DrG = -ln(10)*R*T*log10K,
where R = 8.31451 J/K/mol and T = 298.15 K, we obtain -5708.042*log10Ks
= 29683 or log10Ks = -5.200207. The difference between
solubility product given in thermodynamic data and that retrieved from
dual-thermodynamic activities computed by GEMS is therefore only in the
seventh digit, which is quite accurate.
Now, let us open and re-calculate another system with SysEq record key "NaCl-dep:G:nacl:0:0:1:25:0:". It has the same recipe as the previous one, but with 10 moles of NaCl instead of 0.1 moles. Consequently, even though the Debye-Hueckel equation is inappropriate for such high salt concentration, we expect that the system will be saturated also with halite NaCl solid. Calculation shows that this is indeed the case, as seen from the screenshot provided below.
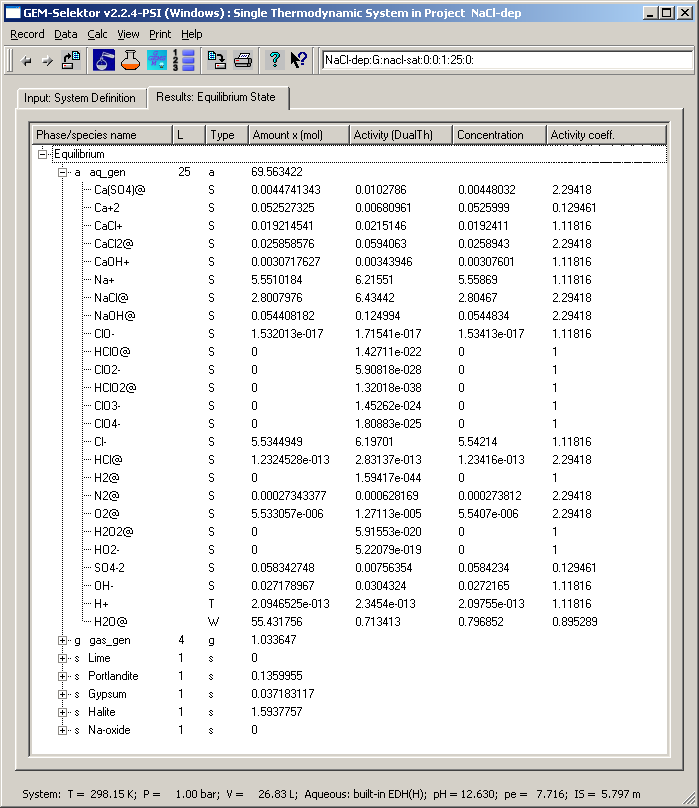
The effective ionic strength of 5.797 m is now quite high and the
total dissolved molality (obtained by subtracting the amount of H2O@
from the total amount of the aq_gen phase) is even greater - 69.563422
- 55.431756 = 14.1317 mol. This is more than the amount of dissolved
halite (10 - 1.5937757 = 8.406224 mol) because of dissociation of NaCl
to ions. The calculated volume of aqueous phase is 1.1589 dm3; from the
molar mass of halite, 58.4428 g/mol, we find that 491.283 g NaCl were
dissolved, or 424 g/dm3. This is greater than the experimental halite
solubility - 360 g/dm3 at 25 C - which shows that the ion-association
model with EDH(H) activity coefficients is not wrong, but also not
accurate at such high salt concentration.
Strong non-ideal effects are expected in this system because the
mole fraction of water is only 0.796852 and the water activity
coefficient is 0.895289. However, the product of these two numbers
(0.713413) is still equal to water activity in the "Activity (DualTh)"
column. The same truth holds for other components (e.g. Na+, difference
only in 6th digit) and the retrieved equilibrium constants of
reactions. Checking this is left to the user.
Please, note that running this project with GEMS versions older than
2.2.4 rc7, you will get slightly different results which will be more
inconsistent in the second, highly concentrated system.